Çoğumuz Sen Ayrı Trende, Ben Ayrı Garda şarkısını duymuştur, hatta bazılarımızın favori listesindedir. Alice ayrı bir trende, Bob ayrı bir gardayken ve Eve mesajları okumaya çalışırken Alice ile Bob güvenli bir iletişimi nasıl başlatabilir? Bu yazımızın konusu bu olacaktır.
Daha önceki yazımızda simetrik şifreleme algoritmalarından ve algoritmaların gizli olmamasının gerekliliğinden bahsetmiştik. Şimdi simetrik algoritmaları da, asimetrik algoritmaları da ilgilendiren anahtar değişimi konusuna değineceğiz. Şifrelemede gösterilen örneklerde Alice ve Bob şifreli bir iletişim oluşturmaya, Eve ise bu iletişimi dinlemeye ya da araya girmeye çalışır. Daha önceden bir araya gelip ortak bir anahtar belirlemeyen Alice ve Bob’un, Eve’e yakalanmadan iletişim kurması için anahtar değişimi gerçekleştirmesi gerekmektedir. Bizim örneğimizde Eve sadece dinleyici konumundadır, araya girip gönderilen mesajları değiştirememektedir. Çünkü bu ele alınması ayrı bir konudur, bizim bugünkü konumuz değildir.
Önceden anahtar belirlemeden güvenli bir tünel oluşturma problemi bizi Diffie-Hellman anahtar değişimi yöntemine getirir. Bu yöntem ilk defa 1976 yılında Whitfield Diffie ve Martin Hellman tarafından “New Directions in Cryptography” makalelerinde yayımlanmıştır. Günümüzde halen kullanılan bir yöntemdir ancak daha fazla geliştirilmiş ve modern varyantları kullanılmaktadır. Mantığı kavrama açısından geleneksel yöntemi incelemek faydalı olacaktır. Khan Academy’nin Diffie-Hellman Anahtar Değişimi videosunun çok güzel bir şekilde açıkladığını düşünüyorum. Şimdi biz bu durumu farklı sayılarla tekrar ele alıp bir nevi ispatını yapalım ve irdeleyelim.
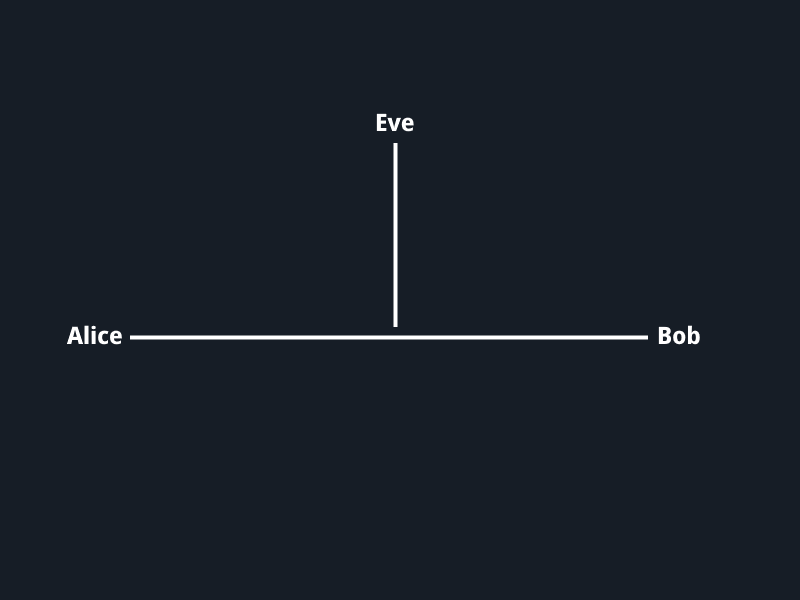
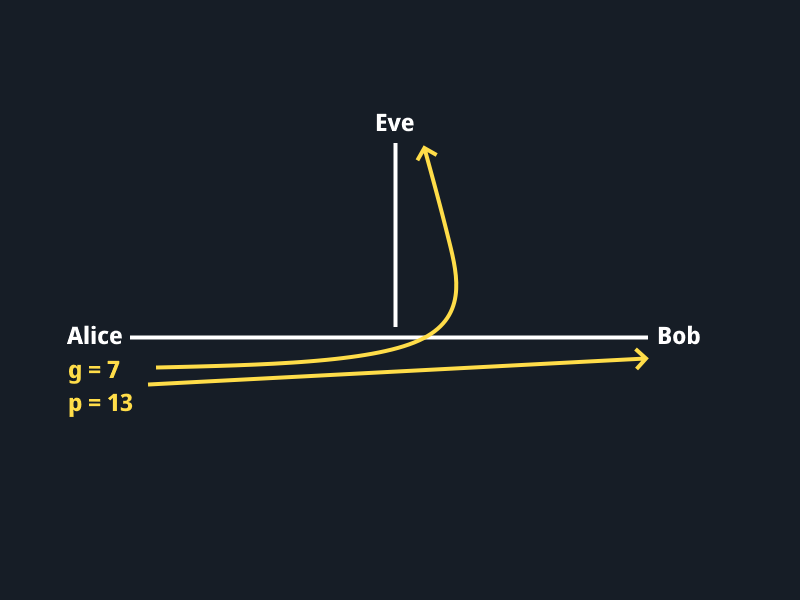
İlk durum yukarıdaki şekildedir. Alice g ve p asal değerleri belirler. Bunu Bob da yapabilirdi, farketmez. Alice g için 7, p için 13 değerlerini belirlemiş olsun. Herkese açık bir şekilde bu sayıları paylaşsın. Aşağıdaki görselde görüleceği üzere Eve de bu sayıları biliyor.
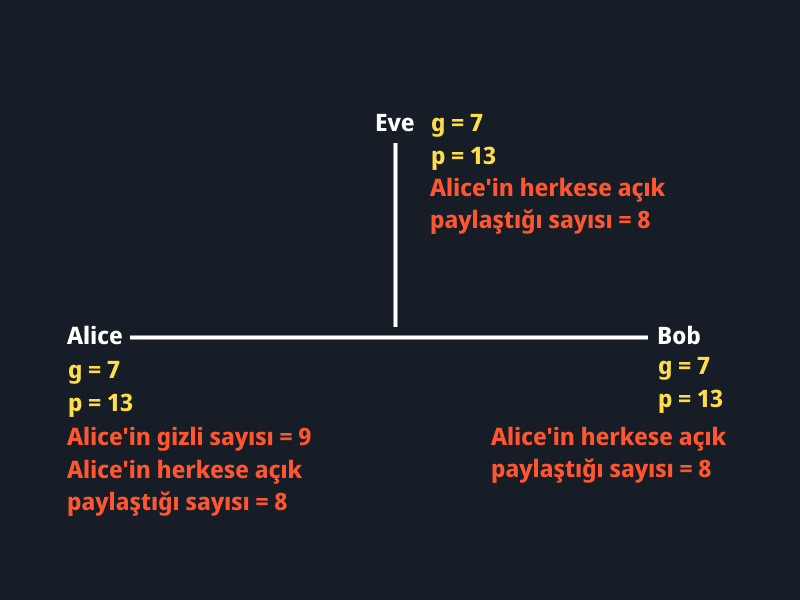
Şimdi Alice’in gizli bir değer belirlemesi gerekiyor. 9 sayısını seçmiş olsun. 7^9 mod 13 işlemini yaptığında ortaya 8 değeri çıkıyor. Bu 8 değerini herkese açık şekilde paylaşıyor. Mevcut durumda Alice, Eve ve Bob’un elde ettiği bilgiler şu şekildedir.
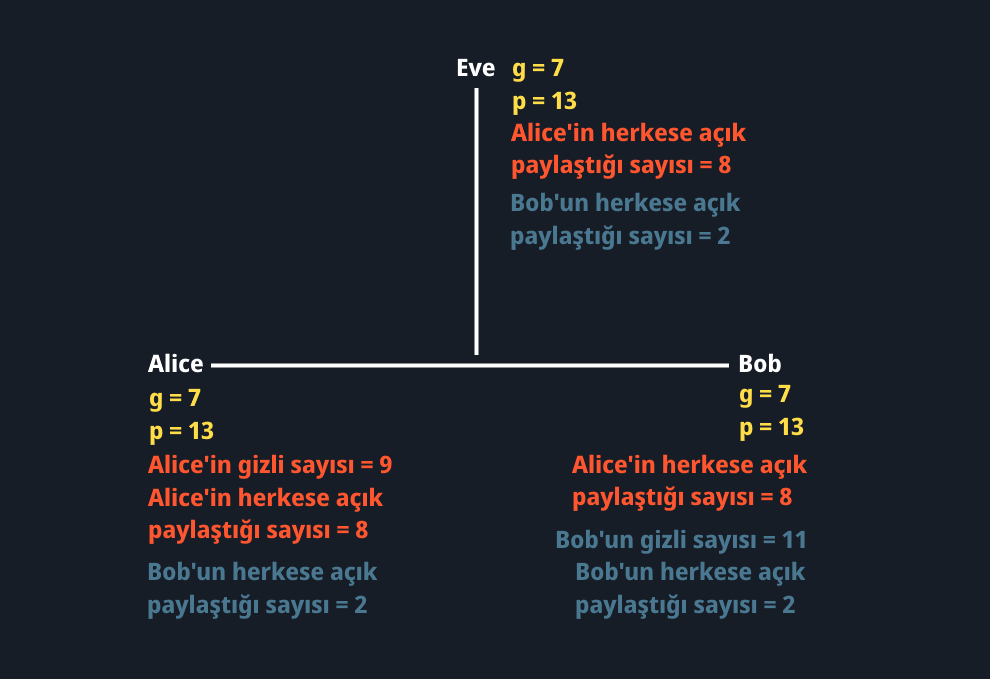
Şimdi benzer bir işlemi Bob yapacaktır. Bob gizli sayı olarak 11 seçmiş olsun. 7^11 mod 13 işlemini yaptığında 2 sayısını elde eder. Yani Bob’un herkesle paylaştığı sayı 2 olacaktır. Son durum aşağıdaki şekilde olacaktır.
Mevcut durumda Alice ve Bob’un ortak anahtarlarını elde etmek için yapması gereken bir işlem daha var. Karşı taraftan aldığı sayı üssü kendi gizli sayısını, p değeri ile mod almalıdırlar. Aşağıdaki görselin daha iyi açıklayacağını düşünüyorum.
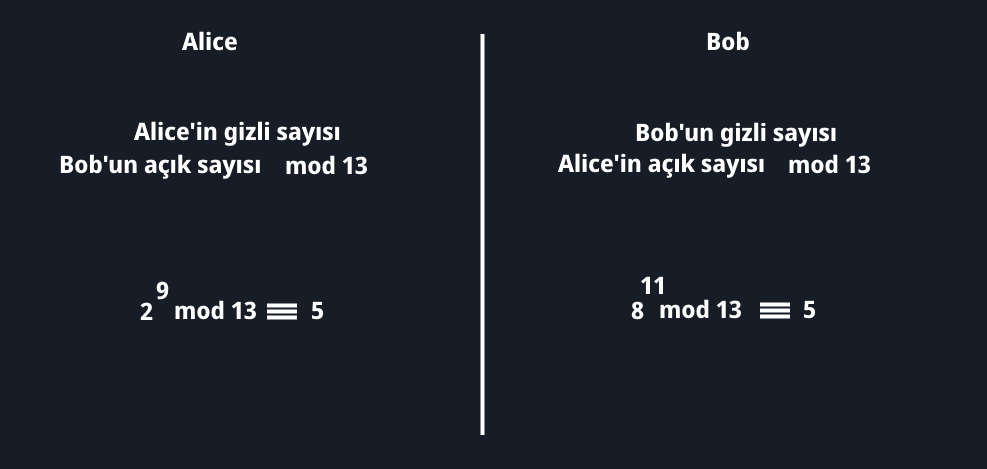
Görüleceği üzere Alice ve Bob anlattığımız yöntemle aynı değere ulaştılar. Eve’nin 7, 13, 8 ve 2 değerleriyle bu sayıya ulaşması mümkün değildir. Örneklerdeki sayılar küçük olduğu için kaba kuvvet saldırısı ile çözülebileceği düşünülse de, gerçek hayattaki kullanımında bu kadar küçük sayılar kullanılmamaktadır. Büyük sayılar kullanıldığında ortaya çıkan değer ile şifrelenmiş metinin makul süreler içerisinde kırılması pratikte imkansızdır. Peki bu durum nasıl gerçekleşti?

Öncelikle son adımı açıklayalım. Üsler ile alakalı olan bu durumda, aynı sayının iki üssünün olması durumunda sonuç birbirlerine eşittir. Yani (3^4)^5 ile (3^5)^4 sayıları birbirlerine eşittir. Bu temel matematik kuralının yanı sıra Diffie-Hellman’ı mümkün ve güçlü kılan başka teoremler mevcuttur. Olaya Eve tarafından bakalım. Büyük sayılar kullanıldığı varsayıldığı için harf notasyonu kullanacağız. g ve p asal sayılarına ek olarak Alice ve Bob’un herkese açık olarak paylaştığı sayılara pa ve pb, gizli sayılarına sa ve sb diyelim.
Eve’in elinde g, p, pa, ve pb var. Eve’in anahtar değerine bu sayılarla ulaşması mümkün değil. Eve’in anahtar değerine ulaşması için sa ve sb sayılarına da ihtiyacı var. Bob’u ele alalım. Bob, herkese açık olarak paylaştığı sayıyı g^sb mod p ile elde etti. Eve’in Diffie-Hellman’ı bildiğini de varsayarsak buradan ilerlemeye çalışabilir. Ama burada bir duvara toslayacaktır: Discrete Logarithm Problem (DLP), namıdiğer Ayrık Logaritma Problemi.
Ayrık Logaritma Problemini basit bir şekilde açıklayalım. Modüler aritmetiği bir saate benzetebiliriz. Örneğimizin problemimizle uyuşması için 12 birimlik bir saat yerine asal bir sayı seçip saatimizin birimini o asal sayı olarak belirleyelim. 19 olsun.

Bir de ipimiz olsun. İpimizin uzunluğu da 45 olsun. Bu ipi tam en üstten saatin etrafına dolamaya başladığımızda ipin ucu 7’ye gelecektir. Bu durumda saatin çevresi modüldür. İpin ucunun denk geldiği nokta sonuçtur. Ayrık logaritma problemine gelecek olursak, modülün bir asal köküyle bu işlemi yapmamız gerekiyor. Bu asal kökün farklı üslerini alıp 19 modülünü uygularsak sonuçlar saatin her noktasına eşit şekilde dağılır. Sonuçtan geri dönmeye çalışacak olursak, yani asal kökün 3 olduğu bir örnekte 3^7 mod 19’un sonucu olan 2’den 7’yi bulmamız çok zordur. Eğer kullandığımız sayılar çok büyük olursa çözüm pratikte imkansızlaşır. Yani Alice ayrı trende, Bob ayrı garda olsa da; ne yollar, ne yıllar, ne de Eve iletişimlerine ayrık logaritma problemi sayesinde gölge düşüremez.
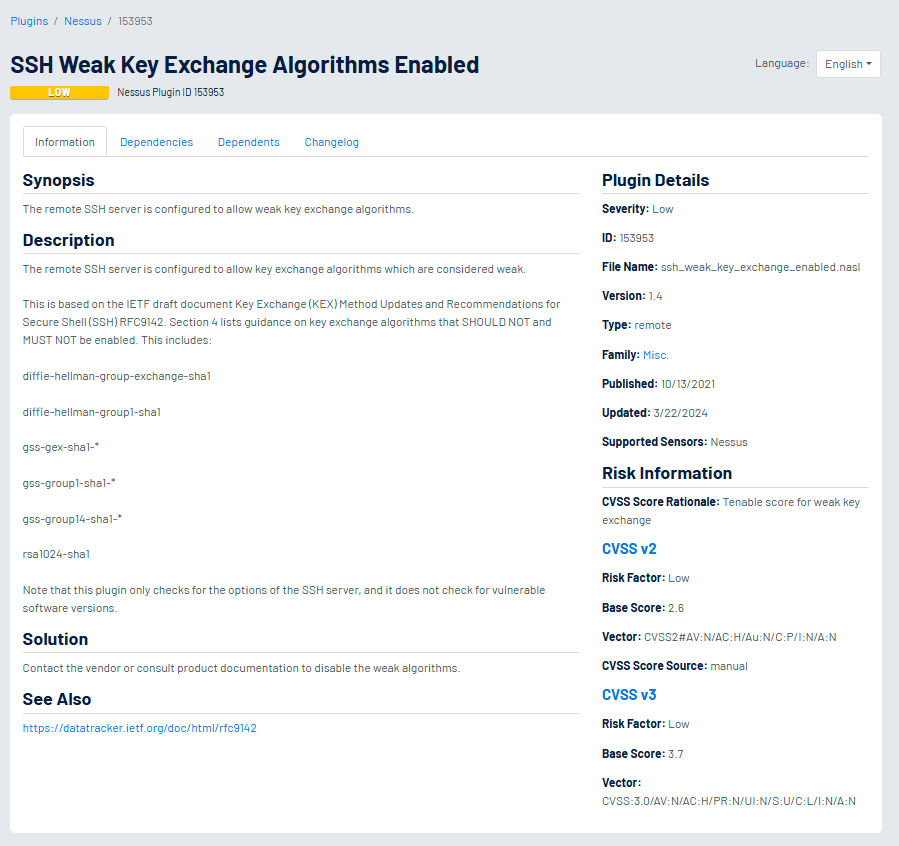
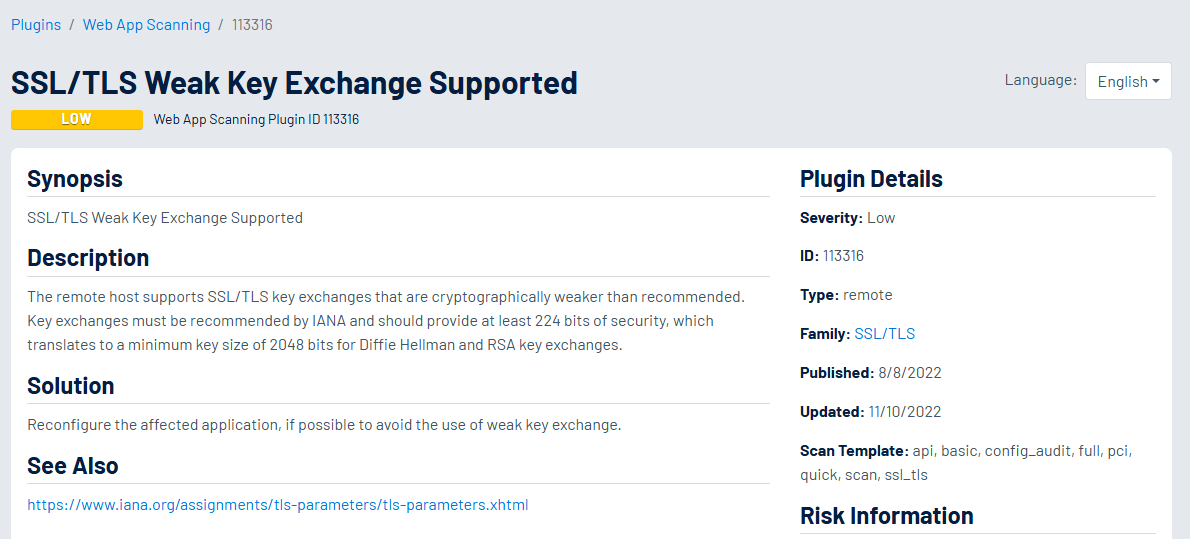
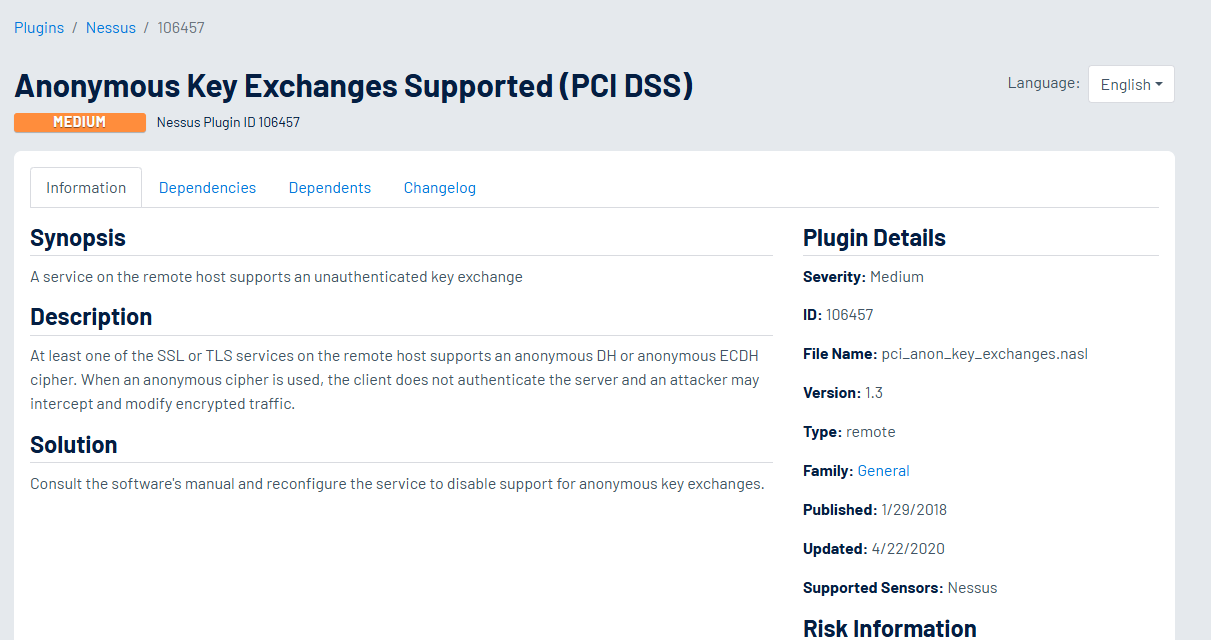
Diffie-Hellman’ın modern varyantlarının günümüzde kullanıldığından bahsetmiştik. TLS, SSH ve IPsec gibi teknolojilerde kullanılmaktadır. Yazımızda belirttiğimiz üzere algoritma güçlü olsa da, bazı yanlış kullanım durumlarında (bizim durumumuzda sayıların küçük seçilmesi zayıflık oluşturuyordu) zafiyetlere sebebiyet verebilir. Aşağıdaki örnekte bir zafiyet tarama aracı olan Tenable Security Center’ın bulabildiği (Tenable Security Center plugin bazlı bir yapıdadır ve tüm plugin ve açıklamalarına Tenable Plugins adresinden erişilebilir) zafiyetler hakkında bilgiler görmekteyiz.